Pythonでカーネル主成分分析を実装してみる

カーネル主成分分析(Kernel principal component analysis; kernel PCA)はその名のとおりカーネルを使って主成分分析(PCA)を行う手法．カーネルっていうのは距離みたいなもん（→Kernel trick - Wikipedia）．線形主成分分析はデータが元の変数のベクトルの線形結合で表されてるとしているけど，そうでもないときもあるよねってことで，非線形写像して主成分分析する．分散共分散行列の代わりに，各データ間のカーネルを要素とするカーネル行列の固有値固有ベクトルを求めるってこと．

Kernel pricipal component analysis - Wikipediaに載ってる画像っぽいのをつくってやってみた．つくったデータ→

kpca.data

"x1 x2 class\n"．3つのクラス．各クラス100個ずつ．

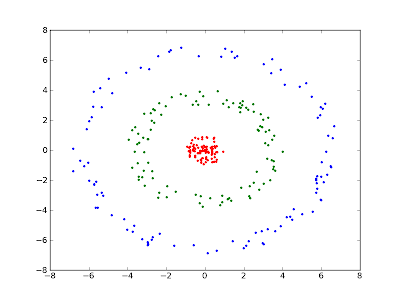
元データの描画．

カーネルは2通り試してみた．固有値大きい方から2つ取り出して固有ベクトルの要素の値をプロット．

その1 多項式カーネル

$$k({\mathbf x},{\mathbf y}) = ({\mathbf x}'{\mathbf y} + 1)^2$$

その2 ガウシアンカーネル

$$k({\bf x},{\bf y}) = \exp \left( \frac{- ||{\bf x} - {\bf y}|| ^2}{2\sigma^2}\right)$$

以下実装．要numpy，matplotlib．



距離（非類似度）行列の固有値固有ベクトル求めて描画するのはMDSっぽい